ДЕФОРМИРОВАНИЕ ПЛАСТИН С ОТВЕРСТИЯМИ ПОД НАГРУЗКОЙ
Миренков В.Е., доктор технических наук
Институт горного дела СО РАН, Новосибирск
Шутов В.А., доктор технических наук, профессор
Новосибирский государственный университет архитектуры, дизайна и искусств
Аннотация: Для пластины с ослаблением, являющейся составной частью многих строительных конструкций, рассмотрена первая и вторая основные задачи в определении Мусхелишвили. Определены граничные значения функции Колосова-Мусхелишвили, описывающие напряженно-деформированное состояние пластины с ослаблением. Приведены результаты численной реализации полученных уравнений.
Ключевые слова: пластина, граничные условия, напряжения, смещения, уравнения, решение.
В рассматриваемых ниже задачах предполагается использовать экспериментальное подтверждение модельных представлений. Такие проблемы возникают при интерпретировании разрушения, экспериментального определения констант материала, расшифровки фотоупругих моделей и др.
Самостоятельный интерес представляет проблема адекватного описания деформирования образцов пород в виде пластин на разрушение, которые хорошо описываются в рамках предлагаемых в работе уравнений, позволяющих следить за изменением напряжений и соответствующих смещений, добиваясь на математической модели воспроизведения эксперимента.
В общем случае рассматривается пластина с граничными условиями в рамках всех трех основных задач теории упругости. Такая пластина представлена на ил. 1., контур которой Г = Г1 + Г2 + Г3 + Г4 + Г5 = Г11 + Г2 ограничивает область S. Нормальные и касательные напряжения и смещения на Г обозначены индексами, связанными с участками Гi = 1,2,…,5 границы. Если участки Г2, Г3, Г4 отсутствуют, то область S занимает полуплоскость с отверстием. Для полосы с отверстием имеем Г = Г1 + Г2 + Г3.
Будем считать, что пластина стоит вертикально и участок Г3 или его часть контактируют с некоторой опорой. В общем случае на Г3 зададим некоторые функции, моделирующие граничные условия. Сказать о них более определенно можно, если только постулировать условия взаимодействия на контакте с оcнованием. Не будем перечислять бесконечное множество ситуаций нагружения пластин, так как все они подпадают под общий случай формулировки граничных задач теории упругости.
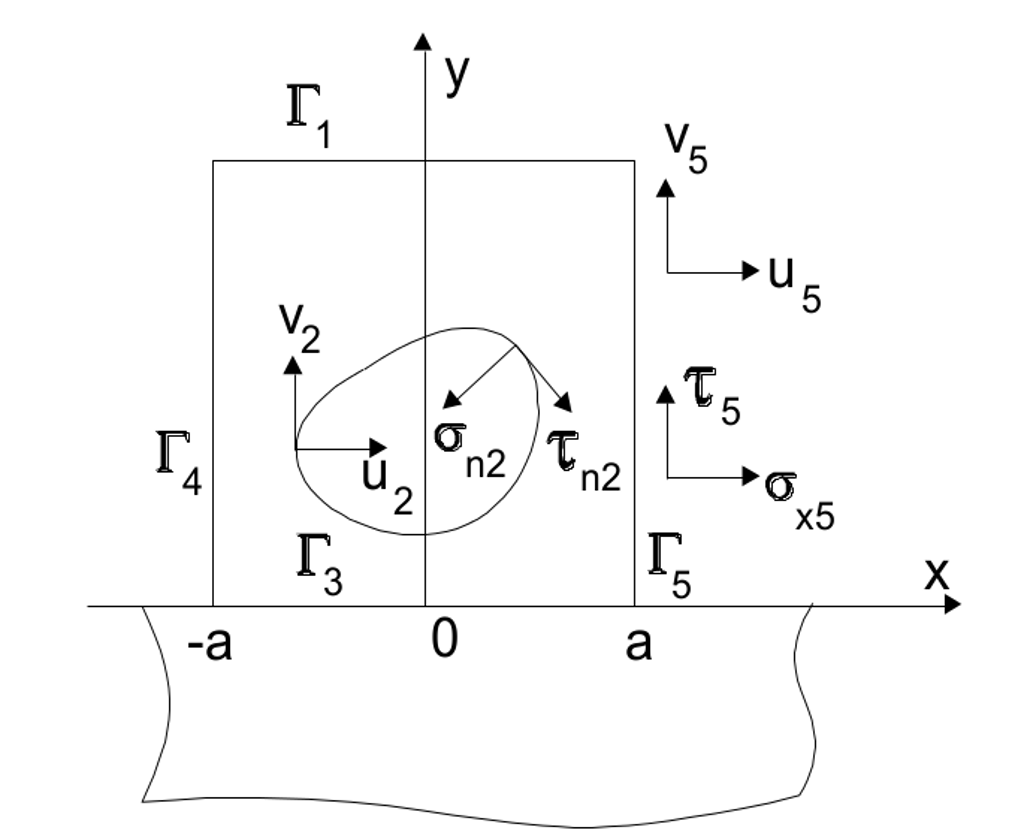
Ил. 1. Схема пластины с ослаблением и граничными условиями для основных задач
В случае первой основной задачи граничные условия для области S запишем в виде [1]

Подставляя (4) в (5), приходим к соотношению, которое связывает граничные значения напряжений и смещений:
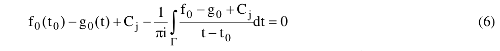
Недостающее уравнение найдем, учитывая, что решение любой основной задачи определяется одной и той же функцией Ψ(z), голоморфной в S. Умножим (1) на к и сложим с (2), в результате получим

Разделяя действительную и мнимую части (6) и (12), можно прийти к двум эквивалентным системам уравнений, то есть для решения задачи можно брать любую из них.
Система (6), (12) позволяет вычислить по заданным граничным значениям любой из основных задач граничные условия для остальных двух, так что в результате на Г известны Xn, Yn , u, v.
Переход в область S осуществляется формулой Коши для функций Ψ(z) и φ(z), получаемых, соответственно, из граничных значений (4) и (7).
В ряде случаев пластину либо подставку под нее можно моделировать полуплоскостью, например, пластина при испытании на изгиб лежит на изолированных опорах, которые в рамках контактных задач [1] можно моделировать как штампы, вдавливаемые в полуплоскость. Деформирование около таких опор, если и рассматривается, то при дополнительном предположении, что на контакте имеет место идеальное проскальзывание. Это предположение на практике никогда не реализуется, какой бы тип смазки не применялся, то есть на контакте возникают всегда касательные напряжения. В общем случае они не будут антисимметричны относительно оси симметрии опоры. Чтобы определить их на контакте, необходим эксперимент.
Для иллюстрации высказанного утверждения обратимся к контактной задаче о вдавливании плоского штампа в полуплоскость. Напряженно-деформированное состояние на контакте с полуплоскостью определяется соотношениями [2]:
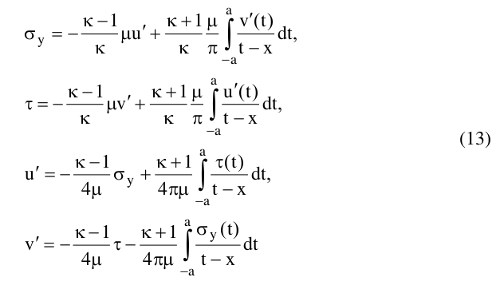
где к, μ – упругие постоянные, штрих означает производную по x. Известны решения об идеальном проскальзывании и сцеплении, представляющие предельные случаи, которые, как отмечалось выше, никогда не реализуются. Если принять, что под штампом возникли касательные напряжения в виде:
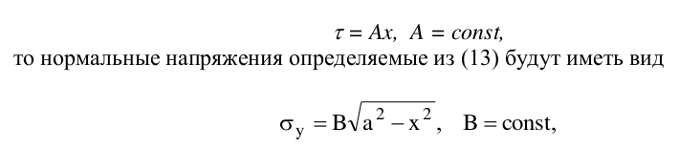
что во всех отношениях ближе к истине, нежели бесконечные классические решения, приведенные, например, в [1].
Методы решения прямых задач, входящих тем или иным образом в общую постановку, приведенную на ил.1, рассматривались в различных работах. В [3] задача для полуплоскости c круговым отверстием дает поле напряжения в области S. Можно поставить задачу по уменьшению, например максимальных напряжений на Г, до некоторого приемлемого уровня, то есть это уже, по существу, обратная задача, и именно они в механике представляют наибольший интерес.
В качестве примера реализации рассматривается случай пластины, когда Г3, Г4 и Г5 отнесены в бесконечность. Граничные условия для такой области S сформулируем в виде:
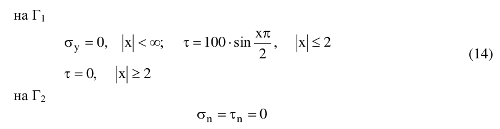
Здесь Г2 – окружность единичного радиуса, центр которой находиться на расстоянии, равном 3 от границы Г1. На ил. 2а приведено расчетное поведение σx на Г1, а на ил. 2б показано распределение напряжений на контуре отверстия: σx – сплошная линия, σy – пунктирная, τ – штрих-линия.
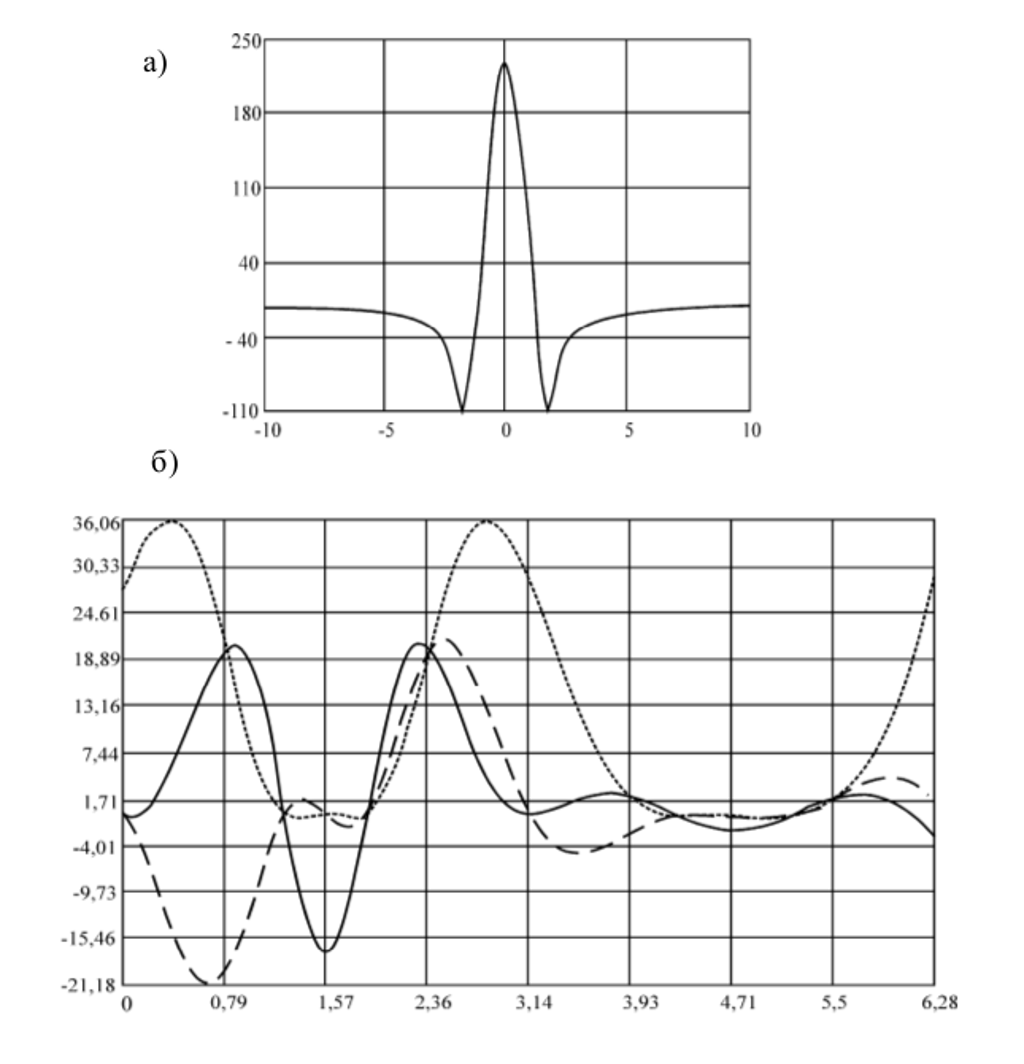
Ил. 2. Эпюры напряжений для задачи (14): а – sx на Г1; б – σx , σy и τ на Г2
Для той же геометрии области S рассматривалась задача с граничными условиями:
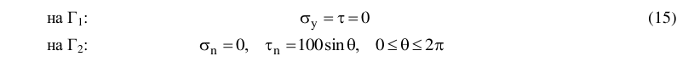
Результаты расчетов приведены на ил. 3.
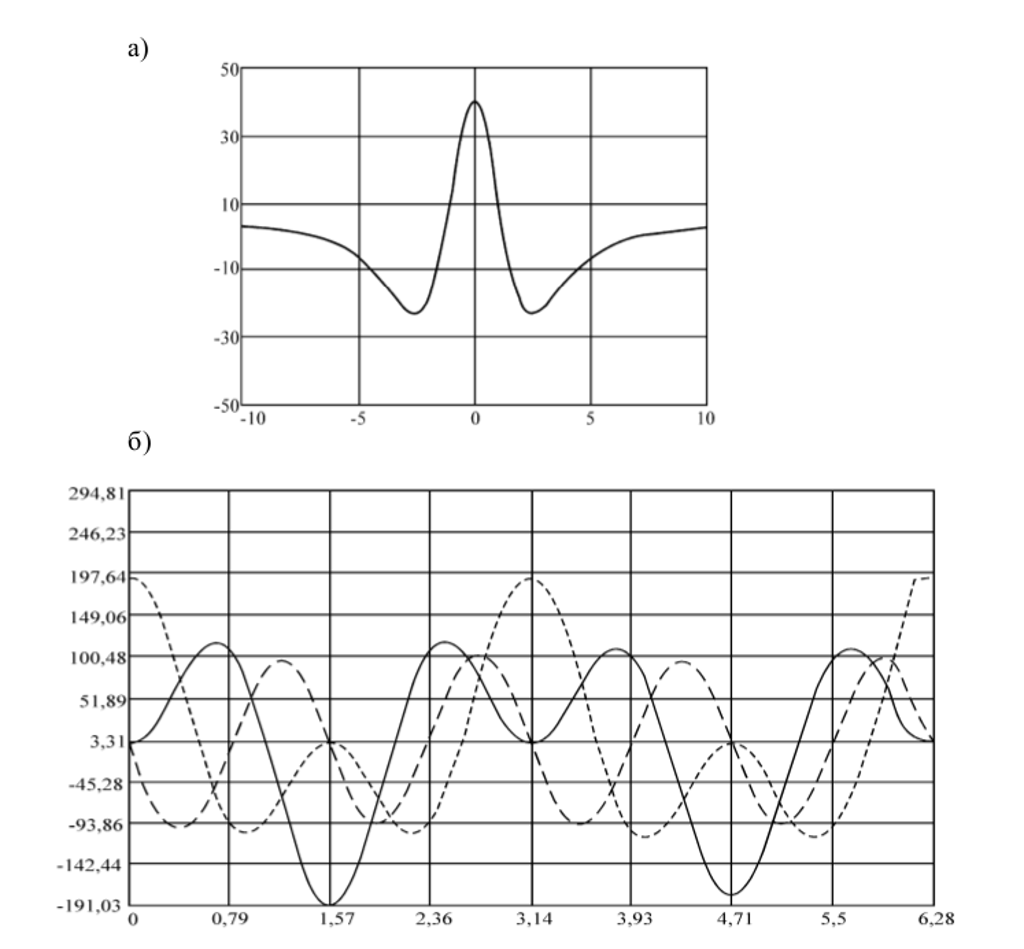
Ил. 3. Эпюры напряжений для задачи (15): а – sx на Г1; б – σx , σy и τ на Г2
Касательные напряжения (14) вызывают значения σx на Г1, достигающие величины 226,6 при х = 0. Представляется возможным, создавая подкрепление Г1, обеспечивающее τ(x) заданного вида, например (14), и нулевые значения σy(x), уменьшить растягивающие напряжения σx, способные вызвать разрушения границ. Этого же эффекта можно добиться, создавая крепь на Г2, обеспечивающую условия, например (15). Как и следовало ожидать, максимальные значения на ил. 2а превосходят соответствующие на ил. 3а.
Библиографический список
1. Мусхилишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 707 с.
2. Курленя М.В., Миренков В.Е., Шутов А.В. Расчет напряженного состояния массива горных пород с использованием натурных данных о деформировании // ФТПРПИ. 1999. №3. С. 27–35.
3. Миренков В.Е., Шутов В.А. Напряженное состояние полуплоскости, ослабленной круговым отверстием // Известия вузов. Строительство. 2000. №12. С. 12–17.
4. Курленя М.В., Миренков В.Е., Шутов В.А. Особенности деформирования пород в окрестности выработки на больших глубинах // ФТПРПИ, Наука. Новосибирск. 2014. №6. С. 3–10.
DEFORMATION OF PLATES WITH HOLES UNDER LOADING
Mirenkov V.E., Doctor of Engineering Sciences
Institute of Mining of SB RAS, Novosibirsk
Shutov V.A., Doctor of Engineering Sciences, Professor
Novosibirsk State University of Architecture, Design and Arts
Abstract: A plate with a weakening is a constitutive part in many building structures. First and second problems, as defined by Muskhelishvili, are considered for the plate. Boundary values of the Kolosov-Muskhelishvili function are defined, which describe the stress-strain state of the plate with a weakening. Results of the numerical implementation of the obtained equations are presented.
Keywords: plate, boundary conditions, stresses, displacements, equations, solution.

